Déclinaison magnétique 

Il y a une notion difficile à assimiler pour les scouts qui se servent d'une boussole : c'est celle de la déclinaison magnétique. Le Nord qui est indiqué sur les cartes est le nord géographique. Il s'agit du pôle Nord et ne correspond pas au nord magnétique indiqué par l'aiguille aimantée d'une boussole.

Explication

Les lignes de forces magnétiques qui suivent la surface de la terre ne sont pas des grands cercles parfaits, mais elles suivent plutôt un itinéraire capricieux en convergeant vers les pôles à cause de sa forme, de la nature de son sous-sol et pour de multiples autres raisons. On leur donne le nom de méridiens magnétiques. Il y a donc un écart entre les lignes des méridiens magnétiques et les lignes des méridiens géographiques. Cet écart porte le nom de déclinaison magnétique. Le long d'une certaine ligne imaginaire qui traverse les grands lacs et la Floride, la déclinaison est de zéro degré. C'est-à-dire qu'à cet endroit, les lignes des méridiens magnétiques et des méridiens géographiques se superposent. Mais partout ailleurs, ces lignes se distancient et il faut tenir compte de la déclinaison avant de suivre un parcours carte-boussole.

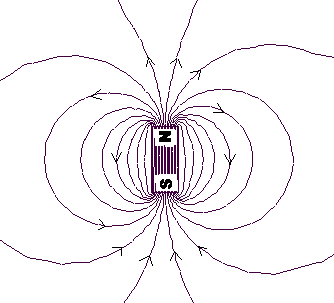
Le champ magnétique terrestre
s'apparente à celui d'un aimant

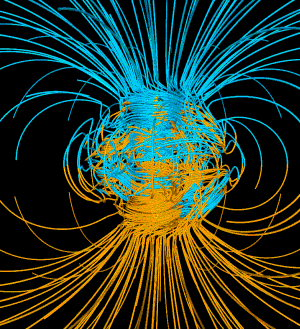
Simulation du champ magnétique terrestre

Calcul de la déclinaison

La position du nord magnétique variant d'une année à l'autre, il faut donc en tenir compte lors du calcul de la déclinaison. Il est facile de calculer la déclinaison magnétique. En voici les étapes :

1. Se référer aux indications pour la déclinaison magnétique
   (informations en marges de la carte).
2. Relever la déclinaison indiquée selon l'année de référence
   (exemple : 2018 = 18°36' 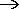18 degrés, 36 minutes)
3. Trouver la différence entre l'année en cours et celle où la déclinaison a été relevée.
   (exemple: 2024 - 2018 = 6 ans)
4. Se référer à la variation annuelle de la déclinaison magnétique.
   (exemple : décroissante 1°5')
5. Multiplier le nombre d'années par le changement annuel.
   (6 * 1°5' = 6°30')
6. Prendre la déclinaison de 2018 et soustraire le résultat obtenu en 5
   (parce qu'au point 4, on a dit que la déclinaison était décroissante)
   (18°36' - 6°30' = 12°6')

Pour une déclinaison croissante (positive ou Ouest), on additionne.
Pour une déclinaison décroissante (négative ou Est), on soustrait.

La déclinaison actuelle est donc de 12°6' alors qu'il y a 6 ans, elle était de 18°36'. Lorsqu'on utilise cette donnée sur une boussole de base, pour tout résultat obtenu, on arrondira au degré près. On inscrira donc 12°.

Les arrondis se font comme pour la base 10 (système décimal).
Exemple de l'arrondi à l'unité près : 1,5 à 1,9 = 2 tandis que 1,1 à 1,4 = 1.

Pour la base 60 (degré/minute), le milieu (0,5), c'est 30'.
Exemple de l'arrondi au degré près : 12°1' à 12°29' = 12° et 12°30' à 12°59' = 13°.

Sachant cela, il devient facile de passer des degré décimaux aux degrés minutes, selon les besoins et l'échelle de la carte.

45,504167°

On prend la portion décimal des degrés pour trouver les minutes
0,504167 * 60 = 30,25002 minutes

On récupère la partie décimale des minutes pour trouver les secondes
0,25002 * 60 = 15,0012 secondes (on va dire 15!)

45,504167° = 45° 30' 15"

Comment additionner, soustraire ou multiplier des degrés et des minutes

C'est souvent à cette étape qu'on perd bien des gens!

Addition et multiplication

1. On additionne (ou multiplie) les degrés avec les degrés, les minutes avec les minutes.

   Exemple :	A)	22° 34'		B)	134° 43'		C)	44° 43'
   +		5° 45'	x		2°   2'	+		3° 17'
   		27° 79'			268° 86'			47° 60'

2. Si la somme des minutes excède 60' inclusivement, c'est qu'on doit rajouter un degré en retranchant 60 au total des minutes. Le reste sera les minutes restantes (parce qu'un degré = 60 minutes).
   
   Donc en A) 79' - 60' = 19' + (1°). Le résultat final est 28° 19'.
   Donc en B) 86' - 60' = 26' + (1°). Le résultat final est 269° 26'.
   Donc en C) 60' - 60' =   0' + (1°). Le résultat final est 48° (inutile d'inscrire 0').

Soustraction

1. On procède de la même manière qu'une soustraction ordinaire.

   Exemple :
   	36° 29'
   -
   	5° 15'
   	31° 14'

2. Tout comme pour une soustraction ordinaire, si on n'a pas assez, on doit emprunter.
   Au lieu d'emprunter une dizaine, on empruntera 60
   (puisque 60 secondes = 1 minutes; 60 minutes = 1 degré).

   Exemple : 18° 16' - 13° 52' 4° 24'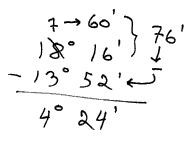

   On ne peut pas retrancher 52' à 16'.
   On doit emprunter 1 degré, ce qui rajoutera 60 minutes à la colonne des minutes.
   Donc 60' + 16' = 76'. Et 76' - 52' = 24'.
   Quant aux degrés : 18° - (1°) - 13° = 4°.

Le même raisonnement s'applique dans le cas des secondes. On retranchera une minute pour rajouter 60 secondes à la colonne des secondes.

Symboles

°		degré
'		minute
"		seconde

Calcul de la déclinaison magnétique en fonction du nord cartésien

Tel que nous l'avons vu dans la rubrique des 3 nords, certaines cartes topographiques peuvent donner la déclinaison magnétique en fonction du nord cartésien et non pas du nord géographique. Légèrement embêtant puisque la déclinaison de la boussole est l'angle entre la déclinaison magnétique et le nord géographique et non pas du nord cartésien.

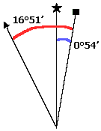
Premièrement, il faut connaître la vraie déclinaison magnétique : entre la boussole et le nord géographique. Nous avons ici la déclinaison magnétique par rapport au nord cartésien. Il faut donc procéder à une soustraction : la déclinaison magnétique réelle est égale à la déclinaison de la carte (16°51') moins la déclinaison du quadrillage (0°54').

Donc, 16°51' - 0°54' = 15°57'

À présent, il faut tenir compte de la variation annuelle :

Année en cours (2024) moins année de référence (2014) = 10 ans.

Variation annuelle (0,1') fois le nombre d'années : 0,1' * 10 ans = 1'. Une minute pile de variation. Celle-ci étant décroissante, il faut donc retrancher une minute à 15°54' => 15°53'. On peut donc arrondir au degré près. La déclinaison magnétique réelle est de 16° ouest. La déclinaison est ouest parce que le nord magnétique se trouve à la gauche du nord géographique sur le pictogramme.

Pour une déclinaison ouest, il faut additionner. Pour une déclinaison est, il faut soustraire.

Par exemple, l'azimut 142° sur la carte reporté sur la boussole deviendra 142°+16° => 158°.

Tout cela pour une petite minute de différence. La raison du peu de différence entre le nord cartésien et le nord géographique s'explique par la grande échelle de la carte : la superficie couverte par la carte étant très petite, la marge d'erreur en est donc réduite. Si nous étions sur une échelle 1 : 250 000, la différence serait beaucoup plus grande.

Mis à jour / révisé le 07-10-2019
Signaler une erreur